Lecture 3
Introduction
In Module 3 of Prof. Wyner’s lectures, you saw a graph of Earned Run Average (ERA) against year. Also shown was a line connecting the average ERA in each year.
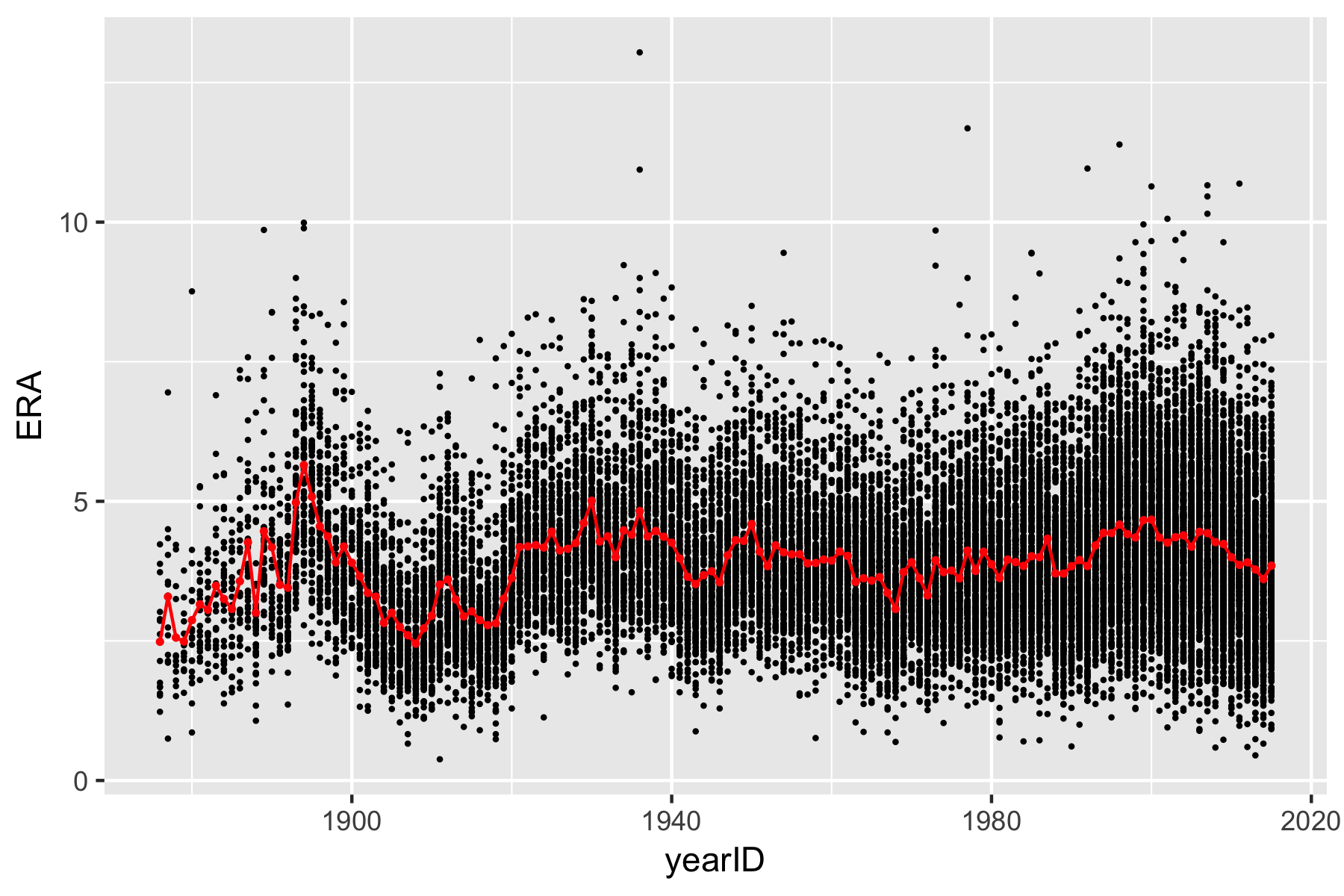
In order to create this figure we need to be able to compute the mean ERA in each year. In the previous exercises, you computed average statistics on a yearly basis by first filtering a tibble and computing the mean of the statistic each time. This was already quite tedious when you did it with the NBA shooting data spanning the 20 years from 1996 to 2016. Imagine trying to do that for each year between 1876 and 2015! Luckily there is an easier way in dpylr.
The Lahman Baseball Database
We will be using the Lahman Baseball Database.
We can load the Lahman database into R along with the tidyverse packages.
> library(tidyverse)
> library(Lahman)We will focus on pitching statistics today.
> data(Pitching)
> Pitching <- as_tibble(Pitching)There are tons of rows and columns in the dataset. For this exercise, we will only want to focus on ERA. We may use select() to pull out the relevant columns. In the Lahman pitching dataset, there is one column named ``IPouts’’ which is three times the number of innings pitched.
We will also focus only on those pitchers with at least 150 innings pitched. Unfortunately, the Lahman dataset does not include innings pitched. Instead, it includes a variable called ``IPouts’’ which is three times the number of innings pitched. Moving forward, we would like to use Innings Pitched, so let us add the column. We also only want to focus on ERA and can ignore the other columns.
> pitching <- Pitching %>% mutate(IP = IPouts/3) %>% filter(lgID %in% c("AL",
+ "NL") & IP >= 150) %>% select(playerID, yearID, teamID, IP, ERA)
> pitching
# A tibble: 9,318 x 5
playerID yearID teamID IP ERA
<chr> <int> <fct> <dbl> <dbl>
1 bondto01 1876 HAR 408 1.68
2 bordejo01 1876 BSN 218. 2.89
3 bradlfo01 1876 BSN 173. 2.49
4 bradlge01 1876 SL3 573 1.23
5 cummica01 1876 HAR 216 1.67
6 deando01 1876 CN1 263. 3.73
7 devliji01 1876 LS1 622 1.56
8 fishech01 1876 CN1 229. 3.02
9 knighlo01 1876 PHN 282 2.62
10 mannija01 1876 BSN 197. 2.14
# ... with 9,308 more rowsGrouped Operations
Instead of summarizing the entire dataset, it is often preferable to summarize the data of individual groups. For instance, we may want to know the average ERA within each year
> pitching.summary <- pitching %>% group_by(yearID) %>% summarize(mean = mean(ERA,
+ na.rm = TRUE), sd = sd(ERA, na.rm = TRUE), med = median(ERA, na.rm = TRUE))
> pitching.summary
# A tibble: 141 x 4
yearID mean sd med
<int> <dbl> <dbl> <dbl>
1 1876 2.42 0.840 2.49
2 1877 2.78 0.805 2.6
3 1878 2.32 0.868 2.06
4 1879 2.57 0.522 2.44
5 1880 2.33 0.710 2.14
6 1881 2.76 0.535 2.54
7 1882 2.76 0.514 2.64
8 1883 2.79 0.771 2.7
9 1884 3.04 1.02 3.04
10 1885 2.87 0.964 2.75
# ... with 131 more rowsWe are now ready to replicate the plot
> ggplot(data = pitching) + ylim(0, 10) + geom_point(mapping = aes(x = yearID,
+ y = ERA), size = 0.3) + geom_point(data = pitching.summary, mapping = aes(x = yearID,
+ y = mean), col = "red", size = 0.6) + geom_line(data = pitching.summary,
+ mapping = aes(x = yearID, y = mean), col = "red")
Standardizing ERA
A Brief Introduction to Writing Functions in R
One really powerful feature of R is the ability to write your own function. Remember, how we can compute the mean, variance, etc? Unfortunately, there isn’t a nice function that returns a vector
> standardize <- function(x) {
+ (x - mean(x))/sd(x)
+ }We can standardize all of the ERAs and plot them:
> pitching <- pitching %>% mutate(zERA_all = standardize(ERA))
> ggplot(pitching) + geom_point(mapping = aes(x = yearID, y = zERA_all), size = 0.3) +
+ geom_hline(yintercept = 0, col = "red")
What do we notice? First, virtually all of the standardized ERAs from the first several years are negative. This would suggest that some of the best pitchers of all time played well before 1900. This is a somewhat ridiculous statement.
Instead, it may be more useful to standardize within each year. We can add a new column to our tibble and then sort it based on the yearly standardized ERA (zERA_year).
> pitching <- pitching %>% group_by(yearID) %>% mutate(zERA_year = standardize(ERA))
> arrange(pitching, zERA_year)
# A tibble: 9,318 x 7
# Groups: yearID [141]
playerID yearID teamID IP ERA zERA_all zERA_year
<chr> <int> <fct> <dbl> <dbl> <dbl> <dbl>
1 leonadu01 1914 BOS 225. 0.96 -3.00 -3.48
2 martipe02 2000 BOS 217 1.74 -2.12 -3.16
3 maddugr01 1995 ATL 210. 1.63 -2.24 -3.02
4 luquedo01 1923 CIN 322 1.93 -1.90 -2.88
5 martipe02 1999 BOS 213. 2.07 -1.74 -2.85
6 brownke01 1996 FLO 233 1.89 -1.95 -2.82
7 eichhma01 1986 TOR 157 1.72 -2.14 -2.81
8 maddugr01 1994 ATL 202 1.56 -2.32 -2.79
9 piercbi02 1955 CHA 206. 1.97 -1.86 -2.77
10 hubbeca01 1933 NY1 309. 1.66 -2.21 -2.77
# ... with 9,308 more rowsWe see now that the best ERA was achieved by …
Of course, we might have decided to group players differently. We could, for instance, divide all of the data into different eras, a la Bill James:
- Pioneer Era: 1871 – 1892
- Spitball Era: 1893 – 1919
- Landis Era: 1920 – 1946
- Baby Boomer Era: 1947 – 1968
- Artifical Turf Era: 1969 – 1992
- Camden Yards Era: 1993 – present
To do this, we need to add an extra column to our tibble that records the historical era. We can do this with mutate() and the case_when() function as follows:
> pitching <- pitching %>% mutate(hist_era = case_when(yearID <= 1892 ~ "pioneer",
+ yearID >= 1893 & yearID <= 1919 ~ "spitball", yearID >= 1920 & yearID <=
+ 1946 ~ "landis", yearID >= 1947 & yearID <= 1968 ~ "baby_boomer", yearID >=
+ 1969 & yearID <= 1992 ~ "art_turf", yearID >= 1993 ~ "camden_yds"))
> pitching <- pitching %>% group_by(hist_era) %>% mutate(zERA_hist = standardize(ERA))Lots of Exercises
- Repeat these types of calculations but with batting statistics – practice adding columns, filtering, grouping, plotting