Stat 7770, Module 02
Richard Waterman
January 2023
Objectives
Objectives
- Jupyter notebooks
- Markdown
-
More Python essentials:
-
Control flow
- Branching
- Iteration
- List comprehensions
-
Control flow
- Summary
Jupyter notebooks
Jupyter notebooks
- Jupyter notebooks are a popular way of facilitating interactive computing and sharing code and results with others.
- You can turn your Jupyter notebook into a slide show (that’s how I make these slides).
- It’s a preferred platform for producing and sharing data science and scientific computing code and results.
- It encourages an interactive exploration of your data.
- It also encourages reproducible research by closely binding data, analyses and results.
- It isn’t just used for Python, so if you use learn other computing languages, you can still probably use Jupyter notebooks.
- You can think of a notebook as an interactive, multimedia script file.
A first look at a notebook and the interface
- Our first task will be to create a new notebook.
- Once created we will look at some basic notebook functionality.
- The key idea is that of “cells”.
- Cells can contain Python code or markdown (a narrative cell).
-
Starting the notebook server will take you to a dashboard from which you can create a new notebook.
- If you already have a notebook on your computer, you can navigate to it via the dashboard and then open it.
Create a folder to store your notebooks
- I have a folder called “Stat_7770_Example_Notebooks” that I will navigate to through the notebooks dashboard.
- Once in the folder, I’ll create a new notebook called “example_one”.
- We’ll do a bit of work in the notebook, create a code cell, some markdown cells, save it, then create a quick presentation.
- As we use the notebooks in subsequent classes, we’ll discuss more functionality.
Cells can be in one of two states
- A cell can either be in the edit or command state.
- When it is in edit state, the border is green.
- When it is in command state, the border is blue.
- You can toggle between states by pressing “enter” and “esc”.
- Clicking either in the cell itself, or the border will have the same effect.
Keyboard short cuts
- Depending on a cell’s state, the keyboard keys will perform different actions.
-
In command mode you can navigate through the notebook, via the arrow keys.
- You can add a cell above or below the current cell with “a” and “b”.
- Delete a cell with d d (or x).
- And bring it back (undo) by pressing z.
- Make it a markdown cell by pressing m.
- Make it a code cell by pressing y.
-
In edit mode:
- The shortcut to run a cell’s content is Ctr-Enter. (Control enter).
-
Ctr Shift - will split the current cell.
- All this functionality is available via the menus too.
- Save the notebook with Ctr-s.
The Jupyter notebook dashboard
- Navigate to the desired directory and create a new notebook.

First tasks
- Rename the notebook as “example_one”.
- Create an initial markdown cell.
- Add a code cell.
- Run the code cell.
- Add another markdown cell.
- Use “View -> Cell toolbar -> Presentation” to get the presentation toolbar menus.
- Identify each cell as a slide.
- Save the notebook (File -> Save and checkpoint).
- Save the notebook as a presentation (File -> Download as -> Reveal.js slides).
- The presentation will be in your downloads folder.
Markdown
Markdown
- Markdown is a light-weight markup language with various flavors for different computing environments.
- It consists of identifiers (tags), that tell how text and images should be later rendered.
- It relies on another program (engine) to actually create the final rendered output.
-
Typical markdown elements include:
- Headers.
- Images and links.
- Lists.
- Mathematical symbols and equations: \(A = \pi r^2\) .
- Tables.
- Word decorations, e.g. italic , bold , emphasis .
- You can render markdown in a Jupyter notebook markdown cell by pressing Ctr-Enter.
- We will use basic markdown. You don’t have to make the output look pretty for the homeworks!
Example markdown cell
- Here is the markdown version of the previous slide:
## Markdown
* Markdown is a light-weight markup language with various flavors for different computing environments.
* It consists of identifiers (tags), that tell how text and images should be later rendered.
* It relies on another program (engine) to actually create the final rendered output.
* Typical markdown elements include:
* Headers.
* Images and links.
* Lists.
* Mathematical symbols and equations: $A = \pi r^2$.
* Tables.
* Word decorations, e.g. *italic*, **bold**, ***emphasis***.
* Tables.
* You can render markdown in a Jupyter notebook markdown cell by pressing Ctr-Enter.
* We will use basic markdown. You don't have to make the output look pretty for the homeworks!Control flow
Control flow and branching
- It is common to want the actions of a program to depend on its inputs, that is, to allow it to branch .
- For example, we may want to perform one action if a variable is a float, and another if it is a string.
- The key command for this conditional execution is “if”.
- It is also common to want to repeat the same action many times, often iterating over each value in some container.
- The key command to do this is “for”.
The “if” statement
If statement schematic

Branching programs with the if statement
- Recall the two logical/boolean variable values, True and False.
- The if statement checks a logical condition and if it is True, executes a block of code.
- It can optionally be followed by other checks, using the “elif” (else if) statement, which if True will execute their own block.
-
Finally, an optional finishing “else” statement will execute when all of the previous conditions are False.
- Syntax-wise, the logical conditions are followed by a colon “:”, and the code block(s) must be indented.
- Many other programs use parentheses to capture a block of code. Python is a bit unusual in using indentation.
The anatomy of an if statement
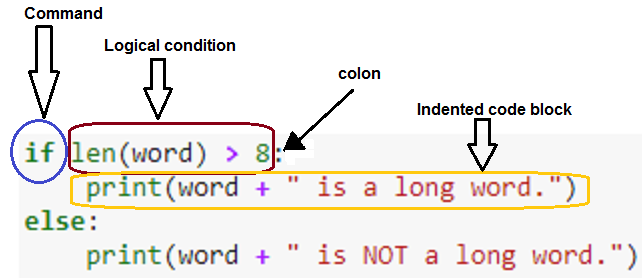
Example using an “if” statement
- The following code looks at a string variable, and if its length (number of characters) is greater than 8, prints a statement to that effect.
- If the word length is not greater than 8, it prints an alternative statement.
word = "Soliloquy"
if len(word) > 8:
print(word + " is a long word.")
else:
print(word + " is NOT a long word.")Soliloquy is a long word.Failing to indent
- If the code block is not indented, an error occurs, so this is not optional!
- Using an IDE will help you avoid this mistake because it will alert you to the problem.
File "C:\Users\water\AppData\Local\Temp\ipykernel_19820\1148153624.py", line 2
print(word + " is a long word.")
^
IndentationError: expected an indented blockA review of logical operations
- We often need to check a number of logical conditions.
- The conditions can be grouped together, most often using the “and” as well as the “or” logical operators.
- For example, we may want to execute a code block if two conditions are simultaneously true (“and”).
- Other times, it may be enough for at least one of the conditions to be true (or).
- The logical operators are “and”, “or” and “not”.
- You may see code written with “&” and “|” in place of and and or . These are “bitwise” operators, but will produce the same results if the elements on either side are the booleans, True and False.
Visualizing the “and” operation

- The shaded area corresponds to A and B being true simultaneously.
The truth table for “and”
- A truth table indicates the outcome of applying a logical operator.
- The “and” truth table is given by:
| X | Y | X and Y |
|---|---|---|
| True | True | True |
| True | False | False |
| False | True | False |
| False | False | False |
Visualizing the “or” operation

- The shaded area corresponds to A or B being true and possibly both.
The truth table for “or”
- A truth table indicates the outcome of applying a logical operator.
- The “or” truth table is given by:
| X | Y | X or Y |
|---|---|---|
| True | True | True |
| True | False | True |
| False | True | True |
| False | False | False |
Verifying the tables
- The following code uses two constructions that are coming up soon.
- “for loops”, and “list comprehension”.
- For now, the idea is to confirm that the truth table is valid! We’ll look at the code more carefully later.
X = [True, True, False, False]
Y = [True, False, True, False]
print([i and j for i, j in zip(X, Y)]) # The "and" (&) truth table[True, False, False, False][True, True, True, False]The not operator
- To turn a True to False, and a False to True, use the “not” operator.
FalseTrueComparison (relational) operators
- It is common to want to compare two numbers, and sometimes strings.
-
The following functions will return a logical value, True or False, so often appear within an
if
statement.
- Are two numbers the same (==).
- Are two numbers not the same (different) (!=).
- Is one number greater than the other (>).
- Is one number greater than or equal to the other (>=).
- Is one number less than the other (<).
- Is one number less than or equal to the other (<=).
Examples
a, b, c, d = 5.1, 12.2, -4, 12.2 # Assign four numbers at once. The right-hand side is a 4-tuple
print(a == b)
print(a != c)
print(b > d)
print(b >= d)
print(c < a)
print(d <= c)False
True
False
True
True
FalseAnother “if” example
- Try the following code, but change what is in the word variable.
- The “elif” block below stands for “else if” and allows for secondary conditions to be checked.
word = "Reasonable"
if (len(word) > 8) and (word[0] == "Y"):
print("A long word beginning with Y")
elif (len(word) > 8) and (word[0] != "Y"):
print("A long word not beginning with Y")
else:
print("Not a long word")A long word not beginning with YAn alternative if else construct
- There is a shorthand for an if-else block, that allows the statement to be written in a single line.
- This is useful if the code block is short.
- The command surrounds the if statement with one expression indicating what to do if it’s True (on the left) and another with what to do if it’s False (on the right).
'long word''short word'Anatomy of the ternary if/else

- The expression to evaluate if the logical clause is True.
- The logical clause.
- The expression to evaluate if the logical clause is false.
The “for” statement
For statement schematic

Anatomy of a for loop
The basic for loop structure looks like this:

- It starts with the “for” command.
- The variable i takes on the values in the collection or iterator (3).
- The collection or iterator.
- A colon to indicate that the code block comes next.
- The code block within the for loop, evaluated as i takes on each value in the container.
Example of a for loop
- The square root data transformation:
data = [7, 13, 21, 3, 8, 12] # Data contained in a list
transformed_data = [] # An empty container to accept the transformed data
for i in range(len(data)): # i will take on integer values, 0, 1, ... 5
transformed_data.append(data[i] ** 0.5) # This is the square root transformation
print(transformed_data) # Take a look at what we have created.[2.6457513110645907, 3.605551275463989, 4.58257569495584, 1.7320508075688772, 2.8284271247461903, 3.4641016151377544]Keeping track of the iteration number
- The function “enumerate” will return a sequence, where each element has both the position in the list and its value at the same time.
- It turns out to be a handy construct, as we will see later.
data = [7, 13, 21, 3, 8, 12] # Data contained in a list
transformed_data = []
for i, value in enumerate(data): # note that two components are being returned, i and value.
print ("Looking at " + str(value) + " in position " + str(i))
transformed_data.append(value ** 0.5 )
print(transformed_data)Looking at 7 in position 0
Looking at 13 in position 1
Looking at 21 in position 2
Looking at 3 in position 3
Looking at 8 in position 4
Looking at 12 in position 5
[2.6457513110645907, 3.605551275463989, 4.58257569495584, 1.7320508075688772, 2.8284271247461903, 3.4641016151377544]Combining for loops and if commands
- This construct is really the beginning of Monte Carlo simulation.
- One way to estimate the probability that an event of interest happens is to simulate many instances of a process.
- For each instance you see if the event happens.
- The number of times that the event happens, divided by the number of instances you simulate is an estimate of the probability that the event occurs.
- As the number of instances get large, then the Law of Large Numbers says that this estimated probability approaches the true probability.
- In this way, we can answer lots of questions for which theoretical approaches are not feasible.
The probability of two aces
- If I shuffle a deck of cards and pull off the top two cards, then what is the probability that they are both aces?
- The code below solves this problem, and we will subsequently dissect it.
import numpy as np # We will use numpy to help shuffle the deck
# Build a card deck (not worrying about the suit)
card_deck = [2, 3, 4, 5, 6, 7 ,8 , 9, 10, 'J','Q','K', 'A'] * 4
# A variable for the number of iterations in the simulation.
num_its = 10000
# A counter to track the number of times the condition (the first two cards are both aces) is true.
counter = 0
# The for loop
for i in range(num_its):
new_deck = np.random.permutation(card_deck) # shuffle the deck.
if ((new_deck[0] == "A") and (new_deck[1] == "A")):
counter = counter + 1
print("The estimated probability of two aces is ", counter/num_its)The estimated probability of two aces is 0.005Comments on the previous code
- numpy is a key library for scientific computing.
- The card deck construction takes advantage of the “*” operation (replicate).
- The event counter is started at 0, prior to the loop.
- A permutation of a set/list rearranges its order.
- A random permutation essentially shuffles the list.
- numpy has a random permutation function.
- The subtlety here is that “new_deck” is a numpy container type called an array , which can only include one type of variable, so the numbers (2 - 10) get turned into strings.
- But that doesn’t impact the answer because we are just looking for the ace (‘A’) value.
- If we use the “+” sign for string concatenation, then the elements on both sides need to be strings, so we cast the numerical answer to a string.
Breaking out of a loop
- Sometimes it is important to be able to break out of a loop.
- The command to do this is break .
- If you have nested loops, then it breaks out of its loop, not all loops.
for i in range(0,5): # The numbers 1 through 4 (outer loop)
for j in range(1,5): # The inner loop.
total = i + j
if total > 4: # break out of the inner loop if the total is greater than 4
break
print ("Outer is {0}, inner is {1}, total is {2}".format(i,j,total)) # More on string formats later.Outer is 0, inner is 1, total is 1
Outer is 0, inner is 2, total is 2
Outer is 0, inner is 3, total is 3
Outer is 0, inner is 4, total is 4
Outer is 1, inner is 1, total is 2
Outer is 1, inner is 2, total is 3
Outer is 1, inner is 3, total is 4
Outer is 2, inner is 1, total is 3
Outer is 2, inner is 2, total is 4
Outer is 3, inner is 1, total is 4The continue command
- If you want to skip the rest of the current iteration, you use the continue command.
- This could be useful if you know that you don’t want to execute the remainder of the code block.
1
3
5
7while statements.
- An alternative to the for statement, is the while statement.
- while looks at a logical condition and executes its code block so long as the condition is true.
- As soon as the condition is false it terminates.
- If the condition is never false, you will have an infinite loop on your hands!
- Here’s the address of the Apple computer company’s old HQ:
One Infinite Loop, Cupertino, CA 95014

Example while statement
x = 0
while x < 6:
print('Keep going, I rolled a {}!'.format(x)) # Note the .format method for the string.
x = np.random.randint(1,7) # This line of code rolls a six-sided die.Keep going, I rolled a 0!
Keep going, I rolled a 2!
Keep going, I rolled a 3!
Keep going, I rolled a 1!- This while loop will keep going until we roll a six.
- At that point the logical condition is false, and the loop terminates.
- In simulation modeling, the while loop can be a useful construct to find out how long it takes until an event of interest happens.
Estimating the expected waiting time until an ace occurs
- Shuffle a deck of cards.
- Deal cards from the top of the deck.
- How many cards do you expect to deal in order to see the first ace (including the ace itself)?
results = [] # start with an empty list to store the results of the experiment.
num_its = 10000 # The number of simulation iterations
for i in range(num_its):
new_deck = np.random.permutation(card_deck) # shuffle the deck.
counter = 1 # a counter for how many cards until the ace is first seen.
while new_deck[counter - 1] != 'A':
counter = counter + 1
results.append(counter)
print("The expected waiting time to the first ace is", sum(results)/num_its, "cards")The expected waiting time to the first ace is 10.6337 cardsComments on the code
- results is a list container into which we will append the number of cards drawn, for each iteration.
- num_its is the number of iterations in the simulation.
- new_deck was defined earlier, and we shuffle it with the help of the numpy package.
- counter will record which sequence number in the deck we are looking at.
- The effect of the inner while loop is that if we don’t see an Ace, then we go keep on going and look at the next card.
- Once we are out of the while loop, we append the counter value to the results container.
- Finally we find the average of the simulations runs, by summing the results list and dividing by the number of iterations.
-
Why do we need to subtract 1 from the counter when looking up the card?
- Because the index of the first element in the list is 0, not 1!
Comprehensions
List comprehensions
- List comprehensions are a way of generating lists in an “elegant” manner.
- They are popular with Python programmers, so you need to be aware of this idiom!
- First we will look at some simple code, review its output, then dig into its parts in more detail.
result_1 = [i**2 for i in range(10)] # The first 10 square numbers.
print(result_1)
result_2 = [i**2 for i in range(10) if (i % 2 == 0)] # Squares of even numbers.
print(result_2)[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
[0, 4, 16, 36, 64]- As you can see above, the code generates a list, possibly subject to a condition (filter).
- It accomplishes the same task as a “for” loop does, but is more compact stylistically.
Anatomy of the list comprehension

- This is the expression that transforms the raw inputs.
- The for loop generates the inputs.
- There is an optional if statement that filters the raw inputs.
Another example of a list comprehension
words = ["This", "is", "a", "list", "of", "key", "words"]
print([word[::-1] for word in words if len(word) > 3])['sihT', 'tsil', 'sdrow']- This code iterates over the words list, assigning each element in turn to the variable “word”.
-
If the length of the word is greater than 3, then:
- the expression reverses the order of the letters in the word.
- Finally, it prints out the new list.
Summary
Summary
- Jupyter notebook introduction.
- A first look at markdown.
-
Control flow
- Branching with if statements.
- Logical and relational/comparison operators.
- Iteration with for and while loops.
- List comprehensions.
- Monte Carlo simulations.
Next time
Next time
- A first look at the pandas library.
-
The Series container:
- Selecting components of a Series.
- Statistical summaries.
-
The DataFrame container:
- Components of a dataframe.
- Creating a dataframe from a dict structure.
- Selecting components of a dataframe (rows and columns).
- Creating more complex logical filters.