ISB
SMMD: Statistical Methods for Management Decisions
Term 1, 2003
Prof. Robert Stine stine@wharton.upenn.edu
444 Huntsman Hall, Statistics Department
University of Pennsylvania
Philadelphia, PA USA 19104-6340
Prof. Richard Waterman waterman@wharton.upenn.edu
400 Huntsman Hall, Statistics Department
University of Pennsylvania
Philadelphia, PA USA 19104-6340
This initial portion of Statistical Methods for Management Decisions introduces you to statistical ideas as they apply to managers. I expect that students taking the course are familiar with basic statistical concepts as covered by Prof. Sukumar in the pre-term basic statistics course (e.g., measures of location and variation, descriptive graphics such as histograms, and the foundations of probability). In these first three weeks, we will consider two basic themes: first, recognizing and describing the variation in everything around us, and then modeling and making decisions in the presence of this variation. The concepts in this course reappear in many other classes and are fundamental in the remaining lectures that describe models that delve into explanations for the presence of variation. It will be worth your effort to understand the ideas, as well as the computational methods and software, from the class.
Statistical Methods for Management Decisions is separated into 14 class sessions. Professor Stine will deliver the first 7 lectures, and Prof Waterman the second set of 7. In the class sessions, I will assume that you have read the assigned sections of the texts. You should also read the introductions of the examples to be covered in the coming class. Our focus is interpreting the meaning of the results in the management context.
You will be using a PC to describe and analyze data using the JMP-IN software introduced by Prof Sukumar. You will find the software manual quite useful. This program resembles a spreadsheet in some ways but has many specialized graphical features not found in Excel and its cousins; working with JMP-IN should have some carry-over value for other courses.
- Foster, Stine & Waterman (1998) Basic Business Statistics. Springer, New York.
- Foster, Stine & Waterman (1998) Business Analysis Using Regression. Springer, New York.
- Supplemental Materials
- Freedman, D., R. Pisani, and R. Purves. Statistics, Third Edition. Norton, New York.
- Hildebrand, D. and L. Ott. Basic Statistical Ideas for Managers. Duxbury, Belmont, CA.
Class Date Lecture Topic
1 Mon May 12 Sources of variation.
2 Tues May 13 Quality control and standard error.
3 Wed May 14 Confidence intervals.
4 Thur May 15 Sampling (and introduction to tests).
5 Mon May 19 Hypothesis testing and making decisions.
6 Wed May 21 Covariance and portfolios.
7 Fri May 23 Correlation, covariance and regression.
8 Mon May 26 Regression assumptions & diagnostics.
9 Wed May 28 Introduction to multiple regression.
10 Fri May 30 Understanding collinearity.
11 Mon June 2 Categorical variables (two levels).
12 Wed June 4 Multilevel categorical variables.
13 Mon June 9 Logistic regression.
14 Wed June 11 Time series.
There will be an exam that covers the material though Lecture 7, and another exam at the end of this course. While the second exam emphasizes the material in Lectures 8-14, this material is inherently cumulative and the ideas of the first seven lectures reappear frequently in later classes.
This class introduces simple, effective ways of describing data. All of the computations and graphing will be done by software. Our task – and it is the important task – is to learn how to interpret the results and communicate them to others. The priorities are: first, displaying data in useful, clear ways; second, interpreting summary numbers sensibly.
The examples of this class illustrate that data from diverse applications often share characteristic features, such as a bell-shaped (or normal) histogram. When data have this characteristic, we can relate various summary measures to the concentration of the data, arriving at the so-called empirical rule. The empirical rule is our first example of a useful consequence of a statistical model, in this case the normal model for random data. Whenever we rely upon a model such as this, we need to consider diagnostics that can tell us how well our model matches the observed data. Most of the diagnostics, like the normal quantile plot introduced in this lecture, are graphical.
Why do data vary? When we measure GMAT scores, stock prices, or executive compensation, why don't we get a constant value for each? Variation arises for many reasons. Much of the statistical analysis of data focuses upon discovering sources of variation in data. Often groups of values can be clustered into subsets identified by some qualitative factor such as industry type, and we can see that the resulting clusters have different properties. Quantitative factors also can be used to explain the presence of variation using methods like regression analysis.
Several examples in this class analyze data that flow in over time. Quite often, a crucial source of variation is the passage of time. Much of the total variation over a period of time often arises from a time trend or seasonal pattern. In the context of quality control, variation arises from the inherent capability of the process as well as from special factors that influence the properties of the output. We will continue our analysis of control charts in the next class.
- Normal distribution, empirical rule, skewness and outliers.
- Multiple boxplots for comparison.
- Trends and seasonality.
- Statistical independence; random variation versus systematic pattern.
- Skewness and variation in executive compensation.
- Patterns in early international airline passenger data.
- Monitoring an automotive manufacturing process.
- FSW, Basic Business Statistics, Class 2-3
Control charts are important tools for insuring quality in manufacturing. This class shows how control charts are constructed and used to monitor various types of processes. The key idea in developing these charts combines the empirical rule from Class 1 with our observation that summary measures such as the mean vary less than the original data. How much less? Today we show how variation in the average, as measured by its standard error, is related to variation in the individual values. We then determine, with the help of the normal model and the empirical rule, how to set one type of control limits.
This is a hard class with some very important concepts that will appear frequently in the rest of this course.
- Populations and samples.
- Parameters (population mean
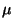 and variance
and variance 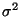 ) and their estimators.
) and their estimators.
- Standard error of the mean (
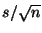 and
and
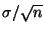 ).
).
- Control limits in quality control charts; alternative rules.
- Central Limit Theorem.
- Control charts for motor shafts (continued).
- Control chart analysis of car trunk seam variation.
- Analysis of production of computer chips (supplemental)
We all sense that large samples are more informative than small ones, because of something vaguely called the “law of averages.” This class considers how to take samples, and explains the basic mathematical results that justify our intuition. The normal distribution plays a key role.
The standard error of the sample average measures the precision of the average and is related to how close one might expect the average to approximate the unknown true process mean. A confidence interval allows us to quantify just how close we expect the sample average to be to the process mean.
After discussing confidence intervals, we introduce several issues in sample survey design. Often, if we are dissatisfied with the width of the confidence interval and want to make it smaller, we have little choice but to reconsider the sample – larger samples produce shorter intervals. Larger samples also cost more and may not be the most efficient way to gather information.
- Confidence vs. precision; confidence coefficient.
- Checking assumptions.
- Simple random sample.
- Questionnaire design and sample validity.
- Randomization and controlled experiments.
- Interval estimates of the process mean (continued).
- Purchases of consumer goods.
- FSW, Class 5
- Review Sections 6.1-6.3; skim Section 7.1; read Sections 7.2-7.4, 7.7.
This class introduces the basic issues concerned with collecting information. The problem of making valid inference about a population based on information obtained in a sample will be the main focus. For this inference to be valid the sample needs to be representative. Though this sounds like common sense, subtle biases often creep in when sampling is done, and when this is the case, the inference may be very misleading. We will discuss some of these biases and explain sampling methods designed to avoid bias.
A key idea is the concept of a random sample. The planned introduction of randomness into the sample allows valid and reliable inferences to be made. Naturally this randomness introduces some uncertainty, but the measures of variability introduced in previous classes provide a means for quantifying this uncertainty.
As time permits, we’ll also start our study of statistical tests during the last hour in this class, so you should also look at the first readings for Lecture 5.
- Sampling: the cost effective way of gathering information about a population.
- Inference about the population; why the sample must be representative.
- Random sampling schemes that ensure a representative sample.
- Sample biases (as the sample size grows the estimates stay bad).
- Non-response and missing data, confounding, length biased samples.
- Hypothesis tests; null and alternative hypotheses.
- False positives and false negatives (a.k.a. Type I and Type II errors).
- One-sided and two-sided comparisons.
- Hotel satisfaction survey.
In quality problems, we need to be assured that the process is functioning as designed, and ideas related to the confidence interval for the process mean are fundamental. In making a decision between two competing alternatives, new issues arise. Statistics provides a number of tools for reaching an informed choice. Which tool, or statistical method, to use depends upon various aspects of the problem. In making a choice between two alternatives, questions such as “Is there a standard approach?”, “Is there a status quo?”, “What are the costs of incorrect decisions?”, “Are such costs balanced?” become paramount.
Often, specially designed tests based on experiments can be more informative at lower cost (i.e., smaller sample size). As one might expect, using these more sophisticated procedures introduces trade-offs, but the costs are typically small relative to the gain in information. When faced with a comparison of two alternatives, a test based on paired data is often much better than a test based on two distinct (independent) samples. Why? If we have done our experiment properly, the pairing lets us eliminate background variation that otherwise hides meaningful differences. Getting proper samples is often simply not possible. Particularly when making two-sample comparisons, one often discovers that the two samples differ in more ways than one expects. In this case study, we consider how such confounding factors influence the outcome of statistical tests and show how, with a little luck and the right questions, we can avoid the worst mistakes.
- Hypothesis tests; null and alternative hypotheses.
- Two-sample and paired tests; experimental design.
- Checking assumptions.
- False positives and false negatives (a.k.a. Type I and Type II errors).
- One-sided and two-sided comparisons.
- Evidence vs. importance; statistical significance versus substantive importance.
- Power of a test.
- Confounding.
- Selecting a painting process.
- Taste test comparison of teas.
- Pharmaceutical sales force comparison.
- Wage discrimination.
- Effects of re-engineering a food processing line. (supplemental)
- Analysis of time for service calls. (supplemental)
Tests based on paired comparisons discussed in Class 5 often are able to detect differences that would require much larger samples without the pairing. Why does this work?
Owners of stock often want to reduce the ups and downs of the value of their holdings – at least they want to reduce the downs! One method for reducing the risk associated with their holdings is to diversify these holdings by buying various stocks. How should the stocks for a portfolio be chosen?
The notion of covariance as a measure of dependence provides a means to answer both of these questions and provides important insights that are fundamental to regression analysis, the key tool developed in the second half of this course.
- Negative and positive association.
- Independent and dependent measurements.
- Covariance and correlation.
- Scatterplot matrix.
- Effect of dependence on the variance of an average.
- Risk reduction via portfolios.
- Building a portfolio.
- Additional handout on portfolios.
This final class reviews the ideas covered in the first 6 lectures, and introduces regression in the context of finance. In particular, we consider how to fit regression lines that model the dependence between two variables, and then relate the slope and intercept of this line to the “beta” of a stock.
- Performance of Mutual Funds
- Value of diamonds
- FSW, Class 11
- FSW, Business Analysis Using Regression, Class 1-3.
Fitting lines and curves to data. Regression model assumptions.
Here we will quantify relationships between variables, both linear
and possibly non-linear. The benefits of fitting a model to data will
be discussed.
Prediction and confidence intervals in regression.
Among the main goals of regression analysis are to predict new observations
(to forecast) and to quantify the uncertainty in these predictions. This class
will discuss the sources of uncertainty in forecasts.
- Plan: second half of Case Book Chapter 2 + Chapter 3
- Review assumptions in regression
- Understanding outliers in regression
- Prediction and confidence intervals
- Display
- Utopia
- Direct
- Cottages
- FSW, Business Analysis Using Regression, Class 2-3.
Many real world relationships are driven by more than a single input variable. For example, costs may be driven by both labor and transportation. Multiple regression extends the idea of simple regression to the situation where there are two or more explanatory variables in the model.
- Prediction and confidence intervals
- Introduction to multiple regression, p.105
- Collinearity - correlated x-variables, p.133
- FSW, Business Analysis Using Regression, Class 4.
Multiple regression offers the potential to isolate the impact of one variable on an outcome variable, controlling for other factors. However, dependence between the explanatory variables, collinearity, means that care must be taken in the interpretation of the regression coefficients. We will study the impact of collinearity, ways to identify its presence in an analysis, and strategies for dealing with it.
- Hypothesis testing for regression slopes - chapter 5 in case book
- Using categorical X's in regression (2 groups) - chapter 6 in casebook
FSW, Business Analysis Using Regression, Class 5.
A key business problem is to compare the average of one variable across divisions of a company. Creating models with these categorical predictor variables allows for comparative analyses such as benchmarking studies. This class will discuss how to include two level categorical predictors in a regression model.
- Hypothesis test examples - chapter 5 in case book
- Using categorical X's in regression (2 groups) - chapter 6 in casebook
- FSW, Business Analysis Using Regression, Class 6.
Not surprisingly, many problems have a categorical variable with more than two levels, for examples sales territories could be divided in North, East, South and West - a four level categorical. Including this sort of variable in a regression is the focus of this class.
- Using multi-level categorical X's in regression (more than 2 groups) - chapter 7 in casebook
- Notice the hyperlink to the example that shows the custom test dialog
for a partial-F test
- FSW, Business Analysis Using Regression, Class 7.
Logistic regression is concerned with modeling a binary outcome variable. A classic example is ``buy'' or ``don't buy'' a product in a marketing study. This technique is extremely useful, but the interpretations are a little harder than in regular regression models. The class will provide an introduction to this sort of modeling and use logistic regression as an example of a ``classifier'', providing for a discussion of classification problems, as opposed to regression problems.
- Regression for a categorical response.
- FSW, Business Analysis Using Regression, Class 11.
Time series data are ubiquitous in business problems. These data-sets often violate the assumptions behind regular regression models. For this reason additional techniques need to be used in order to create a valid and useful model. These time-series techniques will be the subject of this class.
- Modeling time series
- Graphical for autocorrelation
- Durban Watson statistic
- Lags and differencing
- FSW, Business Analysis Using Regression, Class 12.
- Instructors
- Overview. Classes 1-7.
- Materials
- Exams and Grades
- Classes
- Class 1. Sources of variation. Monday May 12
- Class 2. Quality control and standard error. Tuesday, May 13
- Class 3. Confidence intervals. Wednesday, May 14
- Class 4. Sampling. Thursday, May 15
- Class 5. Hypothesis testing and making decisions. Monday, May 19
- Class 6. Covariance, correlation and portfolios. Wednesday, May 21
- Class 7. Regression. Friday, May 23
- Class 8. Regression assumptions and diagnostics Monday, May 26
- Class 9. Introduction to multiple regression. Wednesday, May 28
- Class 10. Understanding collinearity. Friday, May 30
- Class 11. Two level categorical variables in regression. Monday, June 2
- Class 12. Multi-level categorical variables in regression. Wednesday, June 4
- Class 13. An introduction to logistic regression. Monday, June 9
- Class 14. Techniques for modeling time-series. Wednesday, June 11
Richard P. Waterman
2003-05-09